Computer simulation of observable phenomena is an indispensable tool for engineering new technology, understanding the natural world, and studying human society. Yet the most interesting systems are often complex, such that simulating their future behaviour demands storing immense amounts of information regarding how they have behaved in the past. For increasingly complex systems, simulation becomes increasingly difficult and is ultimately constrained by resources such as computer memory.
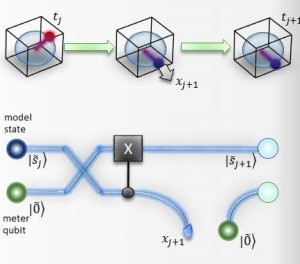
Our previous theoretical work demonstrated that can be broken by quantum processing. This preprint outlines an experimental demonstration of this quantum advantage in simulating stochastic processes. We observed a memory requirement of 0.05 ± 0.01, far below the ultimate classical limit of C = 1. Scaling up this technique would substantially reduce the memory required in simulation of more complex systems.
- Using quantum theory to reduce the complexity of input-output processes
Matthew Palsson, Mile Gu, Joseph Ho, Howard Wiseman, and Geoffrey. Pryde
