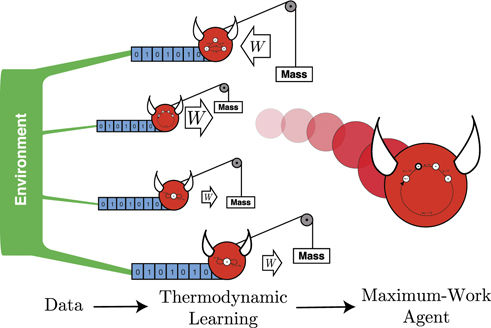
Adaptive systems, ranging from living organisms to autonomous robots, exhibit the ability to thrive by effectively utilizing the resources in their environments. Often this requires learning models of their environment, such that the agent can best understand what to anticipate in the future depending on past expereincces. However, such adaptive systems are physical, and so is there a natural, physical notion of cost?
In this study, we introduce a thermodynamic principle that regards work production as the most significant measure of performance for adaptive physical agents. We compare this principle to the maximum-likelihood approach commonly used in machine learning, which focuses on optimizing model likelihood. e demonstrate that selecting the physical agent capable of maximizing work based on environmental data corresponds to identifying the model with the highest likelihood. This finding establishes an equivalence between nonequilibrium thermodynamics and dynamic learning, revealing work maximization as a fundamental measure of performance that can physically motivate models of machine-learning.
- Thermodynamic machine learning through maximum work production
Alexander B Boyd, James P Crutchfield and Mile Gu, New J. Phys. 24 083040